Основы многокритериального подхода к обоснованию эффективных вложений в недвижимость
28.06.2004
В.Я. Осташко
Сложность процесса инвестирования и многообразие его форм обуславливает необходимость разработки соответствующих методических подходов
Одной из основных проблем экономически обоснованного выбора инвестиционного проекта является сравнение различных вариантов на основе большого числа критериев.
Решению данной задачи посвящено много теоретических и методических разработок, среди которых можно отметить методы, разработанные в рамках теории принятия решений. В самом общем случае данная задача может быть сведена к задаче принятия решений в условиях неопределенности и, в частности, к многокритериальному выбору.
Как известно, многокритериальная модель задачи принятия решений может быть представлена фиксированным набором переменных следующего вида:
<i, S , К, X, f, P, r>, (1)
где i - постановка (тип) задачи принятия решения;
S - множество допустимых вариантов решений;
К - множество критериев, по которым оцениваются решения;
X - множество оценочных шкал;
f - отображение множества допустимых решений во множестве векторных оценок;
Р - система предпочтений лица, принимающего решение;
r - решающее правило.
Решающее правило представляет собой аналитическое выражение, алгоритм или словесную формулировку, которые позволяют задать на множестве векторных оценок отношение предпочтения, являющееся порядком или квазипорядком. Упорядочение множества с помощью векторного решающего правила позволяет перейти от высказывания суждений о предпочтениях на множестве С к высказыванию суждений о предпочтениях на множестве А и, следовательно, дают возможность упорядочить это множество.
В качестве решающего правила в практике используются следующие методы:
- метод простейшего многокритериального ранжирования;
- метод линейной свертки;
- метод "ЭЛЕКТРА";
- метод парных ссравнений;
- метод Терстоуна;
- метод Чермена-Акоффа и др.
Решающее правило должно приводить к такому упорядочению множества допустимых решений, которое соответствует содержательной постановке задачи и согласуется с принятыми в модели допущениями и системой предпочтений лица, принимающего решение.
Построение моделей многокритериальных задач принятия решений является сложной процедурой, состоящей из формализованных и неформализованных этапов.
Для решения задачи выбора наиболее предпочтительного инвестиционного проекта целесообразно использовать следующую последовательность этапов:
1. Формирование допустимых вариантов инвестиционных проектов.
2. Формирование системы критериев (в форме иерархии) для оценки вариантов инвестиционных проектов.
3. Определение коэффициентов относительной важности (весов) каждого из критериев выбора, показывающих, насколько хорошо каждый из них отражает предпочтения лица, принимающего решение.
4. Оценка вариантов выбора в соответствии с критериями.
5. Построение согласованных количественных шкал для каждого из критериев, позволяющих перейти от разных форм представления критериев (количественной, качественной), единиц измерения и направленности влияния на предпочтения принимающих решения к единой шкале.
6. Многокритериальная свертка или определение агрегированных значений (А) вариантов инвестиционных проектов как суммы произведений оценок, полученных по согласованным количественным шкалам, и коэффициентам относительной важности (весам) каждого из критериев.
7. Выбор наилучшего варианта, соответствующего максимальному значению А.
Любой инвестиционный проект сопряжен с определенным риском, который, в свою очередь, может иметь различное выражение и соответствующее измерение.
От того, насколько правильно оценена степень рискованности инвестиций, во многом зависит их эффективность.
Риск, связанный с проектом, характеризуется тремя факторами:
событие, связанное с риском;
вероятность риска;
сумма, подвергаемая риску.
Чтобы количественно оценить риск, необходимо знать все возможные последствия принимаемого решения и вероятность последствий этого решения.
Выделяют два простейших метода определения вероятности.
Объективный метод распределения вероятности основан на вычислении частоты, с которой происходят некоторые события. Частота при этом рассчитывается на основе фактических данных. Так, например, частота возникновения некоторого уровня потерь в процессе реализации инвестиционного проекта может быть рассчитана по формуле:
f(A) = n(А) / n, (2)
где f - частота возникновения некоторого уровня потерь;
n (А) - число случаев наступления этого уровня потерь;
n - общее число случаев в статистической выборке, включающее как успешно осуществленные, так и неудавшиеся инвестиционные проекты.
Субъективная вероятность является предположением относительно определенного результата, который основывается на суждении или личном опыте оценивающего, а не на частоте, с которой подобный результат был получен в аналогичных условиях. Различная информация или различные возможности оперирования с одной и той же информацией объясняют широкое варьирование субъективных вероятностей. Вероятность, равная нулю, означает невозможность наступления конкретного события, вероятность, равная единице, - непременное наступление события. Сумма вероятностей всех возможных вариантов равна единице.
Понятие определенности, неопределенности и риска различаются между собой. Вероятностный инструментарий позволяет более четко разграничить их.
Риск имеет математически выраженную вероятность наступления потери, которая опирается на статистические данные и может быть рассчитана. Чтобы количественно определить величину риска, необходимо знать все возможные последствия какого-нибудь отдельного действия и вероятность самих последствий. Вероятность означает возможность получения определенного результата. Применительно к экономическим задачам методы теории вероятностей сводятся к определению значений вероятности наступления событий и к выбору самого предпочтительного события из возможных, исходя из наибольшей величины математического ожидания. Иначе говоря, математическое ожидание какого-либо события равно абсолютной величине этого события, умноженной на вероятность его наступления.
В самом общем случае величина риска (степень риска) измеряется двумя критериями:
- среднеожидаемым значением результата;
- характером колебания (изменчивостью) возможного результата.
Наиболее часто используемый показатель - средняя арифметическая, определяемая по следующей формуле:
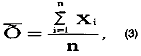
где Xi - наблюдаемые значения результата;
n - число наблюдаемых значений.
Для анализа часто используется также коэффициент вариации. Он представляет собой отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений, которая измеряется в процентах.
![]()
Коэффициент вариации - относительная величина. Поэтому на его размер не оказывают влияния абсолютные значения изучаемого показателя. С помощью коэффициента вариации можно сравнивать даже колебания признаков, выраженных в разных единицах измерения. Коэффициент вариации может изменяться от 0 до 100%. Чем больше коэффициент, тем сильнее колебания значений. Установлена следующая качественная оценка различных значений коэффициента вариации:
до 10% - слабая колеблемость;
10-25%- умеренная колеблемость;
свыше 25% - высокая колеблемость.
Для обоснованного принятия решений в условиях риска разработано большое число методов, среди которых применительно к принятию инвестиционных решений можно выделить следующие:
метод ожидаемой полезности ("платежная матрица");
метод "дерева решений";
метод сценариев;
метод имитационного моделирования (метод "Монте-Карло");
анализ чувствительности проектов.
Суть метода ожидаемой полезности сводится к определению интегрального критерия ожидаемой полезности Ej для каждого i-гo варианта проекта:
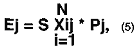
где Xij - результат (например, NPV инвестиционного проекта) для i-гo инвестиционного проекта при условии наступления j-гo состояния внешней среды;
Pi - вероятность наступления j-гo состояния внешней среды.
Критерием выбора наилучшего инвестиционного проекта является максимизация Ej.
Как правило, затраты, производимые во время реализации проекта, требуют осуществления финансовых вложений не единовременно, а в течение определенного, достаточно длительного промежутка времени. Такое положение вещей дает менеджеру возможность проводить переоценку своих вложений и оперативно реагировать на изменение условий реализации проекта.
Риск по проектам, при реализации которых инвестирование средств происходит в течение длительного периода времени, может быть оценен с помощью дерева решений.
Например, фирма собирается инвестировать средства в реконструкцию недвижимости. Инвестиции в данный проект производятся в три этапа.
1 этап. В начальный момент времени необходимо потратить условно 500 у.е. на проведение маркетингового исследования рынка по определению функционального назначения недвижимости и разработке укрупненных вариантов инвестиционных проектов.
2 этап. Если в результате исследования будет выяснено, что потенциал рынка довольно высок, то компания инвестирует еще 1000 у.е. на разработку бизнес-плана.
3 этап. Непосредственная организация процесса инвестирования.
Для анализа многостадийных решений чаще всего используется метод дерева решений (рис.1). В данном случае предполагается, что очередное решение об инвестировании принимается компанией в конце каждого года. Каждое "разветвление" обозначает точку принятия решения либо очередной этап. Использование указанного метода особенно актуально при проведении текущих ремонтов административных зданий с поэтажным графиком проведения строительно-монтажных работ.
| t=0 | t=1 | t=2 | t=3 | t=4 | t=5 | 1=6 | "Совместная вероятность" | NPV | Итого: Prob* NPV |
| 10000 | (10000) | (10000) | (10000) | 0.144 | 15250 | 2196 | |||
| (10000) | 4000 | 4000 | 4000 | 4000 | 0.192 | 436 | 84 | ||
| (1000) | 2000 | 2000 | 2000 | 2000 | 0.144 | (14379) | (2071) | ||
| (500) | 0.320 | (1397) | 447 | ||||||
| Стоп | 0.200 | (500) | (100) | ||||||
| NPV= (338) |
Если по результатам маркетингового исследования компания приходит к оптимистическому заключению о потенциале рынка, то каждый последующий этап работ может удорожаться, в том числе за счет дополнительных поступлений от эксплуатации недвижимости.
При этом операционные потоки наличности в течение срока жизни проекта будут зависеть от того, насколько хорошо капитализированная недвижимость будет "принята" рынком.
Предположим, что ставка цены капитала компании при реализации данного проекта составляет 11,5%, и по оценкам финансовых менеджеров компании реализация данного проекта имеет риск, равный риску реализации типичного "среднего" проекта компании. Умножая полученные значения чистой приведенной стоимости на соответствующие значения совместной вероятности, мы получим ожидаемую чистую приведенную стоимость инвестиционного проекта.
Если ожидаемая чистая приведенная стоимость проекта получилась отрицательной, то компания, казалось бы, должна отвергнуть этот инвестиционный проект. Однако, на самом деле подобный вывод не так однозначен. Необходимо еще учесть возможность отказа компании от реализации данного проекта на определенном этапе или стадии, что может привести к существенному изменению одной из ветвей дерева решений.
Отметим, что финансирование инвестиционных проектов - это динамичный процесс. В каждой узловой точке дерева решений условия реализации проекта могут измениться, что приводит к автоматическому изменению чистой приведенной стоимости (NPV).
Суть "метода сценариев" заключается в следующем:
- по каждому проекту строят три его возможных варианта развития: пессимистический, наиболее вероятный и оптимистический;
- по каждому из вариантов рассчитывается соответствующий NPV, то есть получают три величины: NPVp, NPVml, NPVo;
- для каждого проекта рассчитывается размах вариации NPV по формуле:
(NPV) = NPVo - NPVp, (6)
- из двух сравниваемых проектов тот считается наиболее рискованным, у которого больше размах вариации NPV.
В табл.1 показан пример расчета на основе метода сценариев для двух проектов, имеющих одинаковые ежегодные денежные поступления.
Таблице 1
Пример определения предпочтительности проекта на основе метода сценариев
| Показатель (у. е.) | Проект А | Проект В |
| Инвестиции | 9,0 | 9,0 |
| Экспертная оценка среднего годового поступления: | ||
| пессимистическая | 2,4 | 2,0 |
| наиболее вероятная | 3,0 | 3,5 |
| оптимистическая | 3,6 | 5,0 |
| Оценка NPV (на основе расчета): | ||
| пессимистическая | 0,10 | -1,42 |
| наиболее вероятная | 2,37 | 4,27 |
| оптимистическая | 4,65 | 9,96 |
| Размах вариации NPV | 4,55 | 11,38 |
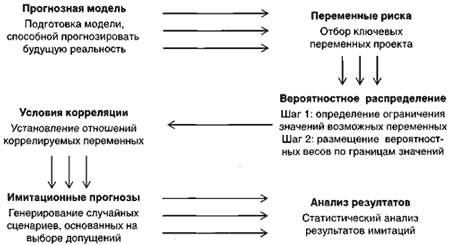
Рис.2, Блок-схема алгоритма имитационного моделирования по методу Монте-Карло
Таким образом, проект В предполагает больший NPV, но в то же время он более рискованный.
Существуют модификации рассмотренного метода, предусматривающие применение других количественных вероятностных оценок. В этом случае:
- по каждому варианту рассчитывается пессимистическая, наиболее вероятная и оптимистическая оценки денежных поступлений и NPV;
- для каждого проекта значениям NPVp, NPVml, NPVo присваиваются вероятности их осуществления:
- для каждого проекта рассчитываются вероятное значение NPV, взвешенное по присвоенным вероятностям, и среднее квадратическое отклонение от него;
- проект с большим значением среднего квадратического отклонения считается более рискованным.
Имитационное моделирование по методу Монте-Карло позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию), получить распределение доходности проекта.
Блок-схема, представленная на рис.2, отражает укрупненную схему работы с моделью.
Применение метода имитации Монте-Карло предполагает использование специальных прикладных программ пакетов (например, RISK, Risk-Master). Фактически метод имитационного моделирования Монте-Карло представляет собой "воссоединение" методов анализа чувствительности и анализа сценариев на базе теории вероятностей. Результатом такого комплексного анализа выступает распределение вероятностей возможных результатов проекта (например, вероятность получения NPV<0).
Первый шаг при применении метода имитации состоит в определении функции распределения каждой переменной, которая оказывает влияние на формирование потока наличности. Как правило, предполагается, что функция распределения является нормальной, и, следовательно, для того, чтобы задать ее, необходимо определить только два параметра - математическое ожидание и дисперсию.
После определения функций распределения можно переходить непосредственно к применению процедуры Монте-Карло, которая включает в себя следующие этапы:
1. В соответствии с вероятностной функцией распределения, генерирующей случайные значения с заданным законом распределения, определяется значение потока наличности, либо определяются переменные, которые являются, в свою очередь, параметрами определения потока наличности.
2. Выбранное значение случайной величины, наряду со значениями переменных, являющимися экзогенными переменными, используется при подсчете чистой приведенной стоимости проекта.
Шаги 1 и 2 повторяются большое количество раз, например 1000, и полученные 1000 значений чистой приведенной стоимости проекта используются для построения плотности распределения величины чистой приведенной стоимости со своим собственным математическим ожиданием и стандартным отклонением.
Задача аналитика, занимающегося анализом риска, состоит в том, чтобы хотя бы приблизительно определить для исследуемой переменной (фактора) вид вероятностного распределения. При этом основные вероятностные распределения, используемые в анализе рисков, могут быть следующими: нормальное, равномерное, треугольное и др.
В процессе каждой итерации происходит случайный выбор значений ключевых переменных из специфицированного интервала в соответствии с вероятностными распределениями и условиями корреляции. Затем рассчитываются и сохраняются результативные показатели (например, NPV).
Завершающая стадия анализа проектных рисков - интерпретация результатов, собранных в процессе итерационных расчетов. Результаты анализа рисков можно представить в виде профиля риска. На нем графически показывается вероятность каждого возможного случая (имеются в виду вероятности возможных значений результативного показателя).
В формализованной записи в общем виде определение "чувствительности" функций описывается значениями первой производной непрерывной функции:
у ` = f ` (x) = dy/dx, (7)
где х - исследуемая на "чувствительность" независимая переменная.
Последовательное использование в качестве аргументов всех характеристик, входящих в формулу показателя-индикатора рисков и последующее определение производных позволяют проранжировать эти характеристики по степени убывания "чувствительности".
Если же имеет место неопределенность (то есть существует возможность отклонения будущего дохода от его ожидаемой величины, но невозможно даже приблизительно указать вероятности наступления каждого возможного результата), то выбор альтернативы инвестирования может быть произведен на основе одного из трех критериев:
1. Критерий MAXIMAX (критерий оптимизма) - определяет альтернативу, которая максимизирует максимальный результат для каждой альтернативы.
2. Критерий MAXIMIN (критерий пессимизма) - определяет альтернативу, которая максимизирует минимальный результат для каждой альтернативы.
3. Критерий БЕЗРАЗЛИЧИЯ - выявляет альтернативу с максимальным средним результатом (при этом действует негласное предположение, что каждое из возможных состояний среды может наступить с равной вероятностью; в результате выбирается вариант, дающий максимальную величину математического ожидания).
Соответственно своему отношению к неопределенности инвесторы подразделяются на пессимистов, оптимистов и нейтральных к неопределенности, они принимают решение о выборе инвестиционного проекта в соответствии со следующими условиями:
временными предпочтениями;
ожидаемой доходностью инвестиционного проекта;
степенью неприятия риска;
вероятностными оценками.
Решение об инвестициях вряд ли будет принято в условиях полной неопределенности, так как инвестор приложит максимум усилий для сбора необходимой информации. По мере осуществления проекта к инвестору поступает дополнительная информация об условиях реализации проекта и, таким образом, ранее существовавшая неопределенность снимается.
Литература.
1. Ворониовский А.В. Инвестиции и финансирование. Методы оценки и обоснования. - СПб.: Изд. С.-Петербургского университета. 1998г.
2. Грабовый П. Г., Уай Т.Н. Конкуренция и управление рисками на предприятиях в рыночных условиях. М.: Алане 1998,
3. Гришин В.К. Статистические методы анализа и планирования экспериментов. - М.: Издательство МГУ, 1975г.
4. Саати Т. Принятие решений. Метод анализа иерархий. Пер. с англ. - М.: Радио и связь, 1993г.
Международный научно-практический журнал "Недвижимость: экономика, управление" №7-8 / 2004